 |
Iowa Section of the Mathematical Association of America |
 |
| 2:30-5:00 |
| 3:00-3:20 | Strong Signals: L(d,2,1)-Labeling on Simple Graphs |
| * Jean Clipperton, Simpson College | |
| An L(d, 2, 1)-labeling is a simplified model for the channel assignment problem. It is a natural generalization of the widely studied L(2, 1) and L(3, 2, 1)-labeling. An L(d, 2, 1)-labeling of a graph G is a function f from the vertex set V(G) to the set of positive integers such that if the distance between vertices x and y is 1, then |f (x)- f (y)| >= d; if the distance between x and y is 2, then |f (x)- f(y)| >= 2; and if the distance between x and y is 3, then |f (x)- f (y)| >= 1. The L(d, 2, 1)-labeling number k_d(G) of G is the smallest positive integer k_d such that G has an L(d, 2, 1)-labeling with k_d as the maximum label. This talk will present general results for k_d when labeling simple graphs, such as paths, bipartite graphs, and cycles. |
| 3:30-3:50 | On the Weakly Sign Symmetric Matrix Completion Problems |
| * Jonathan Botts, Drake University | |
| An n x n matrix is called a P-matrix if all its principal minors are positive. An n x n matrix, A = [a_{ij}], is sign symmetric, if for each i,j \in \{1, 2, \dots, n }, either a_{ij} = 0 = a_{ji}$ or a_{ij}a_{ji}>0; the matrix is weakly sign symmetric if a_{ij}a_{ji}\ge 0. In this talk we show that an n x n partial (weakly) sign symmetric P-matrix specifying an asymmetric acyclic digraph can be completed to a (weakly) sign symmetric P-matrix. We also show that a partial n x n (weakly) sign symmetric P-matrix specifying an asymmetric digraph with no 3-cycles, can be completed to a (weakly) sign symmetric P-matrix for n >= 5. |
| 3:00-3:20 | Computer Explorations of Prime Conjectures Made by Marnell |
| Charles Ashbacher, #none | |
| In 1742, Goldbach made a conjecture that every even integer greater than 2 is expressible as the sum of two primes. While extensive computer searches have failed to find a counterexample, the general conjecture remains open, although nearly everyone believes that it is true. In a recent submission to Journal of Recreational Mathematics, Geoffrey Marnell made ten additional conjectures regarding what can be expressed using prime numbers. This paper gives the results of computer explorations carried out to test the conjectures. |
| 3:30-3:50 | Why Do Students Have Textbooks? |
| Mariah Birgen, Wartburg College | |
| Textbooks should be readable and students should read them! In fact, students should be expected to read the textbook before they come to class!! Reading questions test student's superficial knowledge of pre-class reading while giving teachers just-in-time teaching opportunities to clarify misconceptions. |
| 3:50-4:10 |
| 4:10-4:30 | Sign patterns that allow a positive or nonnegative left inverse |
| In-Jae Kim, Minnesota State University, Mankato | |
| An m x n sign pattern S is an m x n matrix with entries in {+,-,0}. An m x n sign pattern S allows a positive (resp., nonnegative) left inverse provided that there exist an m x n matrix A with sign pattern S and an m x n matrix with only positive (resp., nonnegative) entries satisfying BA=I_{n}, where I_{n} is the n x n identity matrix. Using associated bipartite digraphs, we characterize m x n (m >= n >= 2) sign patterns that allow a positive left inverse. This generalizes the known result for the square case. Some results on sign patterns allowing a nonnegative left inverse are also presented. (This is joint work with D.D. Olesky, B.L. Shader and P. van den Driessche.) |
| 4:40-5:00 | Minimum Rank of Powers of Some Special Graphs |
| Luz De Alba Guerra, Drake University | |
| For an n x n symmetric matrix A the graph of A, G(A) =(V, E) is a simple undirected graph with vertex set {1, 2, ..., n }, where {i, j } is in E, if and only if a_{ij} is not 0. For a graph G, with vertex set V = {1, 2, ..., n }, and edge set E, the r-th power of G is the graph G^r = (V, F), where {u, v } is in F if and only if there is a walk of length r from u to v. The minimum rank of a graph G is mr(G) = min{ rank(A) : A = A^T, and G(A) = G }. In this talk we determine the minimum rank of certain powers of two special families of graphs: paths and trees in general. We will also present a onjecture on the minimum rank of powers of cycles. |
| 4:10-4:30 | Ethics and Standards |
| Henry Walker, Grinnell College | |
| The MAA Committee on the Profession (CotP) has been asked by the MAA Board of Governors to draft a Statement of Ethics Standards. This talk will provide an overview to the work on this project and encourage reactions to the current working draft. |
| 4:40-5:00 | Optimal arrangement of digits |
| Ronald Smith, Graceland University | |
| Problem: Arrange a sequence of mn positive digits into m n-digit numbers whose product is minimized or maximized. We show how to recognize optimal arrangements of digits, and give an efficient algorithm for finding solutions. |
| 5:00-7:20 |
| 7:30-7:50 | Using groups and graphs to create symmetry patterns, Parts 1 |
| Joseph A. Gallian, University of Minnesota, Duluth | |
| Part 1 concerns the problem of traversing an m by n directed grid embedded on a torus so that each vertex is visited exactly once before returning to the starting position. We also consider generalizations and variations on this theme. |
| 8:30-- |
| 8:00-11:25 |
| 8:30-8:50 | Using groups and graphs to create symmetry patterns, Part 2 |
| Joseph A. Gallian, University of Minnesota, Duluth | |
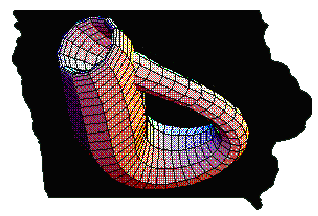
| Part 2 is a discussion of how Hamiltonian paths, spanning trees, cosets in groups, and factor groups can be used to create computer generated symmetry patterns in hyperbolic and Euclidean planes. These methods were used to create the image for the 2003 Mathematics Awareness Month poster. |
| 9:30-9:40 |
| 9:40-10:00 | Teaching tools in the MAA digital library |
| Erick Hofacker, University of Wisconsin - River Falls | |
| The purpose of the workshop was to inform participants of the teaching tools available through the MAA digital library. Participants at the session are able to do some exploring of sites on their own while I am discussing the vast number of resources that are available. |
| 9:45-10:05 | Mathematics for Sustainable Living: Pre-Calculus Basics |
| M Anne Dow, Maharishi University of Management | |
| This talk describes a new math course I am designing for our Sustainable Living students. The purpose of the Sustainable Living major is to equip students to design, build, and maintain sustainable communities. The prerequisite for the new math course is Intermediate Algebra. It will cover simple linear models, exponential and logarithmic functions, graphs of functions, trigonometry of triangles, and elementary probability, all in the context of problems and topics arising in our Sustainable Living major. |
| 10:15-10:35 | The Possible Use of Wavelets in Digital Audio Upsampling |
| Scott Searcy, Waldorf College | |
| The challenge of high fidelity digital to analog conversion of digital audio information is quite challenging. This paper will the possible use of wvaelets to increase the fidelity of the recovered analog signal. |
| 9:45-10:05 | Assimilating Drifter Trajectories using Gradient Descent |
| Neil Martinsen-Burrell, Wartburg College | |
| In geophysics, we frequently try to couple dynamical models of physical systems such as the atmosphere or ocean with direct observations of those systems. In the atmosphere, with fixed observing stations, there are advanced techniques for Numerical Weather Prediction. In the ocean, observations are often made by objects that drift with the flow. This presents difficulties for conventional data assimilation methods. I will discuss one possible way to assimilate drifter trajectories into a very simple dynamical model. |
| 10:15-10:35 | Connected goalies for convex polygons |
| David Romano, Grinnell College | |
| Given a compact convex body K in the plane, call a connected 1-dimensional set G in the plane a goalie if it intersects all the straight lines that intersect K. This talk is concerned with the problem of finding the minimal length goalie for polygons. For any polygon P with n sides, we prove that any shortest goalie G for P has convex hull CH(G) a polygon with at most 2n sides. For triangles T, the minimal length goalie is the Steiner minimal tree for T. This is no longer true in the case of quadrilaterals, in which case a Steiner minimal tree need not be a minimal goalie. |
| 10:45-11:05 | How likely is a lattice link? |
| Dennis Roseman, University of Iowa | |
| Lattice points in space are points with integer coordinates. A unit lattice edge is a line segment of unit length between lattice points. A lattice link is a finite collection union of lattice edges whose union is topologically equivalent to a union of disjoint circles. We define a notion of probability for lattice knots and links and use this to frame the question: which is more ``likely'', the square knot or the granny knot. A square knot is obtained by tying a right hand trefoil and a left had trefoil together; the granny knot is obtained by using two identical trefoils. We also discuss our progress towards calculation of these probabilities. |
| 9:45-10:05 | On a Group Associated With Projective Planes |
| ** James Fiedler, Iowa State University | |
| A pair of orthogonal Latin squares of order n is equivalent to a permutation on the set of ordered pairs of integers 1, ..., n. Since a projective plane of order n exists if and only if there exists a set of n-1 mutually orthogonal Latin squares of order n, the group generated by the above permutations may be of some interest in the study of projective planes. Relevant definitions and results of some investigations concerning these groups will be presented. |
| 10:15-10:35 | Farey Symbols and subgroups of $SL_2(Z)$ |
| ** Chris Kurth, Iowa State University | |
| The structure of subgroups of SL_2(Z) (2x2 integer coefficient matrices with determinant 1) is important in the study of modular forms. Associated to these subgroups is an object called a Farey Symbol which contains the structure of the group in a very compact form. For instance, from the Farey Symbol one can easily calculate an independent set of generators for the group, a coset decomposition, and determine if the group is congruence. In this talk, I will discuss finite index subgroups of SL_2(Z)$ and the computation and use of Farey Symbols for these subgroups. |
| 10:45-11:05 | An algorithm for creating "equal" regions |
| Mark Mills, Central College | |
| This talk will discuss an algorithm that is still in development. The goal of the algorithm is to take a large area that has been broken up into counties and use some quantifiable information for each county (e.g., population) to create a given number of geographically compact regions having relatively equal quantities. The speaker will discuss the evolution of the algorithm from first being a greedy algorithm to now being what you might call an "altruistic" algorithm. |
| 11:25-12:10 |
| 12:10-1:30 |
| 1:35-1:55 | On the Mathematics of Juggling |
| Stephen Willson, Iowa State University | |
| The mathematical analysis of juggling gives interesting examples of permutations and uses of modular arithmetic. Simple mathematical notation can be used to describe many different ways of juggling. The descriptions can tell which periodic patterns give valid juggling methods. |
| 2:05-2:25 | Linear Differential Equations |
| Wolfgang Kliemann, Iowa State University | |
| Spectral properties of matrices can be characterized in various ways: The algebraic approach via the characteristic polynomial yields the eigenvalues and corresponding (generalized) eigenspaces resulting in the Jordan normal form. The linear-algebraic approach using similarity of matrices again re- sults in a characterization via the Jordan form. Furthermore, the dynamical approach via di§eomorphic conjugacy of linear áows eAt x and eBt x again implies similarity of the matrices A and B. If one weakens ídi§eomorphic conjugacyí to íhomeomorphic conjugacyí (or homeomorphic equivalence), homeomorphic conjugacy of eAt x and eBt x is equivalent (in case there are no eigenvalues on the imaginary axis) to the dimensions of the stable (or unstable) subspaces of A and B being equal. In applications, such as nonlinear di§erential equations, one is often in- terested in matrix normal forms that are írougherí than the Jordan form, and Öner than the characterization via stable subspaces: typical examples are the idea of invariant manifolds in dynamical systems theory, or stabil- ity and stabilizability of control systems. These approaches work with the exponential growth behavior of a áow eAt x and are thus interested in the real parts of the eigenvalues and the corresponding subspace decomposi- tion (Lyapunov normal form). While this form can, of course, be derived from the Jordan form, there is no obvious dynamical characterization of the Lyapunov normal form in Rd . In this talk we present dynamical characterizations of the Lyapunov form for matrices by looking at the induced áows on pro jective space and the ex- istence of homeomorphisms which respect the Önest Morse decomposition, i.e., they map Morse sets onto Morse sets and respect their order. It turns out that the Morse sets and their order on the full áag manifold do not characterize the Lyapunov form. Instead, also the pro jections to the Grass- mannians and the order of the corresponding Morse sets has to be taken into account. This results in a constructive characterization via an order graph, which we call the Grassmann graph associated to a matrix. |
| 2:35-2:55 | Preferential Attachment Random Graphs with General Weight Function |
| Krishna B. Athreya, Iowa State University | |
| Start with a graph G_0 = {V_1 , V_2} with one edge connecting the two vertices V_1, V_2. Now create a new vertex V_3 and attach it (i.e. add an edge) to V_1 or V_2 with equal probability. Set G_3={V_1 , V_2, V_3}. Let G_n={V_1,…,V_{n+2}} be the graph after n steps, n>=0. For each i, 1<= i <= n+2, let d(i) be the number of vertices in G_n that V_i is connected to. Now create a new vertex V_{n+3} and attach it to V_i in G with probability proportional to w(d_i(n)), 1 <= i <= n+2, where w(.) is a function from N={1,2,…} to (0, \infty). In this talk we look at some results about the degree sequence {d_i(n)}, n>=1, i>=1 and the empirical distribution {p_n(j) = (1/n)\sum_{i=1}^n I(d_i(n)=j)}, n>=1. |
| 1:35-1:55 | Geometry for the Artist: A General Education Course |
| Catherine Gorini, Maharishi University of Management | |
| This paper will describe the course Geometry for the Artist that I have been teaching for over 20 years at M.U.M. The topics covered symmetry, Euclidean geometry, perspective, fractals, non-Euclidean geometry, and topology. For each topic, we discuss applications in the visual arts with an emphasis on M. C. Escher. This course satisfies the distribution requirement for mathematics. |
| 2:05-2:25 | The Mean-Median Map |
| Marc Chamberland, Grinnell College | |
| Starting with a non-empty finite set S_n={x_1,\ldots,x_n} contained in R, generate the unique number x_{n+1} which satisfies the mean-median equation (x_1 + \cdots + x_n + x_{n+1}/(n+1) = median(S_n) . As usual, we define the median of the set S_n = {x_1,\ldots,x_n}, where x_1<= ... <= x_n, as median (S_n) = \left\{ x_{(n+1)/2}, n odd , \frac{x_{n/2} + x_{n/2+1}}{2}, n even . By applying the mean-median equation repeatedly to a set one generates an infinite sequence {x_k}_{k=1}^\infty. The dynamics of this map are surprising! Most maps tend to have either relatively simple dynamics or chaotic dynamics. While the mean-median map seems to be asymptotically constant, it seems very hard to predict. This talk will showcase the work done to date. This is joint work with Mario Martelli (Claremont McKenna College). |
| 2:35-2:55 | Dots and Lines |
| * Thomas Britton, Coe College | |
| “It's not fair!!!” This phrase echoes of our past playing games as children. This study looks at what it means for a game to be “unfair” and applies it to the common childhood game of Dots and Lines. We look at a triangular board with an eye to extrapolations to other more exotic constructions and use both combinatorial game-theoretic tools and computer analysis to compare to “brute force” conclusions. From this we can conclude this game is unfair and identify certain tactics that can aid the advantaged player in obtaining a victory. |
| 1:35-1:55 | “Hex Play: Do board modifications make a difference in game outcome?” |
| * Evan Jones, Coe College | |
| I conducted research in the summer of 2006 dealing with the game of Hex, the two player combinatorial game developed independently by Piet Hein and John Nash. I wanted to know if modifying the game board by removing available playing spaces would effect the outcome of the game. I analyzed a 3x3 size board, then a 5x5 board, and some preliminary work on a 7x7 board. |
| 2:05-2:25 | Mathematical Questions from the Classroom |
| Wendy Weber, Central College | |
| How can we bridge the gap between prospective teachers' knowledge of mathematics and the mathematics they will teach? In 1987 Richard J. Crouse and Clifford W. Sloyer published the (now out of print) two-volume book Mathematical Questions from the Classroom. Using this book as a guide, a one semester hour course was designed to help pre-service teachers learn how to handle mathematical questions that arise in the classroom. We will explore questions from the middle school level, introductory through advanced algebra, geometry, trigonometry, functions, probability, and calculus. Some questions expand pre-service teachers' knowledge of mathematics while others help them identify and correct typical student mistakes. |
| 2:35-2:55 | Overview of the version of Mathematica currently in development |
| Al Hibbard, Central College | |
| This talk will look at some of the new features that are being developed for the version of Mathematica currently in development. An overview will be given as well as some illustrations of how to exploit some of the new features. |
| 3:00-3:10 |
| 3:10-3:30 | Counting the number of solutions in a finite group |
| Siu-Hung (Richard) Ng, Iowa State University | |
| The notion of Frobenius-Schur (FS)-indicators of a finite group representation has been developed for more than a century. These indicators can be obtained by counting the number of solutions x of the equation x^n=g in a finite group. Moreover, the second indicators can be used to construct topological invariants of surfaces. It was not known until recently that they are invariants of the tensor categories of finite group representations. In the talk, we will give a brief history of these indicators and their new developments. |
| 3:40-4:00 | What I did on my sabbatical: Experiencing the "real world" |
| Mark Mills, Central College | |
| In an effort to gain some "real world" experience with mathematics and statistics during my sabbatical this year, I have been working at a local windows manufacturer doing a number of things that involve mathematical and statistical thinking. This talk will describe some of the things I have been doing, as well as some of the things I have learned through the experience. I will also discuss how I went about setting-up this experience, how I think my employer perceives my experiences, and how I expect this to be something that lasts beyond this year. |
| 3:10-3:30 | Historical Roots of Math and Physics in Germany |
| * Tim Schwickerath, Wartburg College | |
| In May 2006, a class of thirteen students and Dr. Brian Birgen from Wartburg College toured Germany and examined math and physics from a historical perspective. The class toured various musuems and universities all around Germany. The class also explored the German culture through home stays and other experiences. Two students from the class will share and discuss highlights of their experiences. |
| 3:40-4:00 | An Introduction to Minimum Rank of a Graph |
| ** Rana Mikkelson, Iowa State University | |
| Given a graph, we can associate a set of matrices therewith: the set of all symmetric matrices A over R where aij = 0 ? G has an edge between vertex i and j . We define the minimum rank of a graph is then the minimum among the ranks of all the matrices in this set. There is no one easy formula for computing this value given any graph, but for certain types graphs we can find the minimum rank exactly, and for others we can at least determine a few bounds. This talk introduces the topic and begins to explore the known results. |
| 3:10-3:30 | Pseudo-Random Walks |
| Christian Roettger, Iowa State University | |
| In a recent Monthly article, O'Bryant, Reznick and Serbinowska [ORS] have given some fascinating new insights into the behavior of \[ S_{N}(\alpha) := \sum_{n=1}^N (-1)^{[n\alpha]} \] where [x] is the integer part of x. Since the fractional part of n*\alpha for n=1,2,3,\dots behaves 'random-ish', one can make various guesses and apply classical methods like exponential sums to explore these hypotheses. Remarkably, the guesses are often wrong and the classical methods don't seem to work very well. Instead, [ORS] use continued fractions to obtain sharp and explicit upper and lower bounds for |S_{\alpha}(N)| in terms of \log N, and as a by-product get a way of evaluating S_{\alpha}(N) for large N with amazing efficiency.\\ We will explain that last part of their work. Then we will show how to use exponential sums with a twist that gives a lower bound for |S_{\alpha}(N)| - less explicit, but more general than what the methods from [ORS] give you. And if we omit tedious computations (which we will, and which are only long, not hard), the approach is as clear-cut and beautiful as that using exponential sums to the case of the fractional part of n*\alpha. Lit.: K.~O'Bryant, B.~Reznick, M.~Serbinowska: {\em Almost alternating sums}, Monthly vol.~113/8, pp. 673-688. Prerequisites: only complex exponentials e^{it}. |
| 3:40-4:00 | Using Oral Exams to Help Prepare Future Elementary Mathematics Teachers |
| Russell Goodman, Central College | |
| The ability to effectively communicate mathematics is a priority for future elementary mathematics teachers. An oral examination, if used appropriately, is an excellent tool for assessing such skills. Moreover, an oral exam is a useful pedagogical tool for helping future elementary mathematics teachers improve their skills in communicating mathematical concepts.
The speaker has used oral exams in his department's mathematics course for future elementary mathematics teachers and will share the logistical details for how he includes an oral exam component to these courses. Additionally, he will share anecdotal evidence for the pedagogical effectiveness of the oral exams, along with some student feedback. |
* denotes an undergraduate speaker and ** indicates a graduate student speaker