Where: Lamar University, Beaumont, Texas
When: October 7-8, 2016
What: For the past eleven years, undergraduate students have gathered in Huntsville, Tyler, San Antonio, and Nacogdoches to talk about math, play games, and network with students and faculty from around the state of Texas. This year, the TUMC came to Beaumont and was another great success! See you next Fall in San Antonio!
 Follow us on Facebook!
Follow us on Facebook!
Friday, October 7, 2016
5:00-6:00 PM |
Registration |
Lucas Building 1st Floor |
6:00-8:00 PM |
Pizza and Games for Students |
Lucas Building Room 119 |
Saturday, October 8, 2016
8:00-9:00 AM |
Registration/Breakfast |
Lucas Building 1st Floor |
9:00-11:00 AM |
Parallel Student Presentations |
Lucas Building Rooms 113, 114, 117, 118 |
11:00 AM - 12:00 PM |
Plenary Address
Su Doree, Augsburg College
Writing Numbers as the Sum of Factorials |
Science Auditorium |
12:00-1:00 PM |
Lunch |
Lucas Building 1st Floor |
1:00 - 2:00 PM |
Breakout Sessions |
Lucas Building Rooms 113, 114, 117, 118, 119 |
| 2:00 - 3:00 PM |
Parallel Student Presentations |
Lucas Building Rooms 113, 114, 117, 118 |
3:00 - 4:00 PM |
Plenary Address
Mark Tomforde, University of Houston
The Mad Veterinarian Puzzle |
Science Auditorium |
4:00 - 4:30 PM |
Wrap-up and Thanks |
Science Auditorium |
Talk Schedule and Abstracts
Click on the talk for its abstract.
In standard decimal notation, we write each integer as the linear combination of powers of 10. In binary, we use powers of 2. What if we used factorials instead of exponentials? How can we express each integer as the sum of factorials in a minimal way? This talk will explore the factorial representation of integers, including historical connections to permutations, a fast algorithm for conversion, and the secret of the "third proof by mathematical induction." Next we'll extend this representation to rational and then real numbers, ending with some remaining open questions.
There is a collection of problems which have come to be known as "Mad Veterinarian Puzzles." In these problems a Mad Veterinarian has various transmogrifying machines that can turn a single animal into collections of other animals (for example, one machine might turn a single cat into a collection of two dogs and three mice). These puzzles ask whether the Mad Veterinarian can turn certain collections of animals into other collections using the machines. In this talk, I will discuss the Mad Veterinarian Puzzle and some interesting (and unexpected!) connections with groups, algebras, and C*-algebras. I'll assume very little background, and the talk should be accessible to anyone with prior exposure to equivalence relations, linear algebra, and groups.
Applying to graduate school in mathematics or any other discipline is a daunting task. In this session, we will discuss resumes, personal statements, the GRE exam, and how to choose the correct school for you. A significant portion of the time will be left for questions.
There are over 50 Research Experience for Undergraduates (REU) programs in Mathematics. In this session, we will discuss finding the right REU, how to improve your application and what actually goes on at an REU. There will also be plenty of time for questions.
Going to conferences can be a lot of work and a lot of fun. Which talks should I go to? What if I don't understand what the speaker is saying? What should I do between talks? These kinds of questions come up for just about everyone. We will talk about how you can get the most out of your conference experiences no matter what your background is.
Mathematical Puzzle Programs (MaPP) designs annual team-based problem-solving competitions for secondary students, available at no cost for colleges and universities to print and run at their own campus. Our goal is to challenge students to use discovery-base methods for solving mathematical problems while giving them experience with mathematics beyond the usual curriculum.
Based upon local outreach events developed at Auburn University and Lamar University, the MaPP High School Challenge '17 will be hosted by several universities and math camps in the United States and Japan during the 2016-17 school year. This year's MaPP's first Middle School Challenge will debut at Lamar University in November.
In this breakout, we will give you a feel for the types of puzzles students encounter during our events, as well as provide information on how you can download MaPP's free open-source resources or host a MaPP event at your own campus.
Those of us who have chosen to pursue an undergraduate major or graduate degree in the mathematical sciences do so primarily because we love mathematics, be it pure, applied computational, or statistical. Thanks to the growing synergy between mathematics, computation, and applications, becoming a mathematician is also a great career choice. In this breakout session, we will explore some of the many career paths open to mathematicians in business, industry, government, and academia. We will also discuss how to prepare for a career in math, including relevant coursework, interdisciplinary research experiences, enriched doctoral training, and the importance of internships.
We will present a math model that investigates the analytics behind the men's NCAA basketball tournament comparing season statistics and results from previous tournaments.
A graph G = (V,E,F) where V is the vertex set, E is the edge set, and F assigns a pair of vertices to each edge. Given a set of vertex weights, a Thor sequence T is a sequence of graphs on n vertices and m edges such that the vertex weights of G induce the edge-weights of G1, the first term in the sequence, which induces the vertex-weights of G2, the second term, and so on. This research focuses on determining the properties of these sequences.

This work investigates the combination of reinforcement learning and radial basis function neural network (RBFNN) learning to improve the performance of a robot's task execution. Due to the benefits of a controlled environment and controlled variables, the robot has been ported to a simulator called VREP. In the current phase the robot is learning to follow a wall. This machine learning technique uses episodic learning, which only processes the learning algorithms once the state has changed. The state is evaluated using ultrasonic sensors, positioned on the front, left and right sides of the robot. These sensors detect the distance from a solid object, the wall, and the sensor itself. The robot evaluates the distances returned from all sensors and calculates its orientation and distance from the wall, combining them into a state. It processes this state through the reinforcement learning algorithm to decide on an action to take. The knowledge gained through reinforcement learning is then used to train the RBFNN, which refines the actions corresponding to each state to improve the robot's performance. We are currently in the debugging phase. This work is joint with Timothy Holcombe, Greg Year, Hannah Leleux, Logan Smith, Alexander Strong, and Colin Smith. It is funded in party by Exxon Mobil and the Lamar University Office of Undergraduate Research.
This project models the math literacy rates of girls across nations of varying levels of development to find an association between the aforementioned, international economic standing, and women's social status. Here, it is investigated if there are factors which certain nations who are similarly developed have in common and how these factors relate to their respective rates of math literacy in girls.
Standard voting methods rely on deterministic social choice functions to aggregate voter preferences and determine a winner or set of winners. In contrast, lottery voting determines winners by randomly selecting voter ballots. In this talk, we will investigate lottery voting from a mathematical perspective. In particular, we will provide insight into the effects of varying the size of the set of winners and potential strategies for political parties within the lottery voting system.
With the use of dual-energy computed tomography (DECT), we create a pre-reconstruction algorithm for multi-material decomposition (MMD) of x-ray images. This is preferred over the post-reconstruction technique which requires initial correction for beam hardening, which can degrade image quality and restrict accuracy. It can also be shown statistically that our pre-reconstruction method handles mixtures of materials better than that of an implemented post-reconstruction method. Using specific restrictions or iterative methods, we are able to decompose more than three materials.
This study develops a three dimensional model of the density of nutrients, the population of algae and the population of sh in a lake ecosystem to determine the infuence human activity has on these variables. Human activity is defined as the runoff of agricultural fields and drainage of industries and urban regions. With the use of Routh - Hurwitz stability criterion the dynamics of the equilibrium were analyzed and simulated numerically. It was observed that when the density of nutrients is low, there is a stable algae population, which is not sufficient for fish to survive. As the in flow of nutrients is increased gradually the population of sh and algae coexist. However, after the density of nutrients surpasses a certain threshold the population of sh exponentially decrease to extinction as algae population spikes. Thus, the recommendation is to monitor the density of nutrients in lakes so that this this threshold is not passed.
Traditional image processing uses pixels as the basic element. Then operations for image processing are done on the pixels. Many of the models created for image processing are quite advanced. However, a new generation of image processing has developed that considers an image patch. Which in turn has made the strategy for image processing quite simple.
In order to better understand the behavior of soliton waves, we analyze solutions to the Korteweg-de Vries and sine-Gordon equations for the single and multiple soliton cases. Through deliberate manipulation of entries, we notice relationships with the matrices and the representations of solutions. We analyze the matrices in the n-soliton case and its behaviors including multiplicities and minor changes to the entries of the matrices.
Group theory has been studied for centuries by many researchers. For example, Lagrange proved that the cardinality of any subgroup of a given finite group is an integer divisor of the cardinality of that group. This paper defines a new concept related to the group theory, called pseudo-partitions of a group. The main result of our paper proves that removing a subgroup from a pseudo-partition of a group cannot be a subgroup of the given group.
Candy Crush Saga is a game where different colored candies are arranged in a grid. To win or advance to the next level, players must swap adjacent candies in order to match three or more consecutive candies of the same color in a row or column. Valid starting configurations avoid such arrangements of consecutive candies. We explore how many valid configurations there are for an m x n grid using q colors and how many of those grids will contain a move to obtain three, four, or five candies of the same color in a row or column.
TETRIS is a puzzle video game that is played with tetromino pieces on a rectangular well of 20 by 10 cells. We analyze some strategies in which tetrominoes can be played so that a player can play indefinitely. More specifically, we present such strategies for games that involve only two tetrominoes: either the Square and an Elbow or the Square and the Bar. We also see that such strategies do not exist for games that involve only the two Kink tetrominoes and thus all TETRIS games with randomly generated tetrominoes must end eventually. We then explore whether such strategies exist for games that involve different combinations of tetrominoes.
We present a mathematical model of the card game War. This game is played by two or more people with the objective being to win all the cards in a deck. When each player reveals a single card, the person with the highest card wins the battle. When a tie occurs, the players go to war and play additional cards. Using Java to simulate a reasonable amount of games, we collect data, including the number of battles that it takes to win the game and the number of wars occurring in a single game and present statistical analysis for our simulation.
We will present mathematical models that are actually used for counting visitors at the National Parks. We will focus on Yellowstone National Park, in particular, and will perform sensitivity analysis on the People Per Vehicle parameter used by Yellowstone.
We will mathematically model wages over time for men and women across different demographics. We include various job sectors of the labor force, race/ethnicity, age, marital status, and level of education.
A concept of non-standard Lagrangians is introduced and general conditions for the existence of such Lagrangians are presented. The conditions are used to determine classes of ordinary differential equations (ODE's) that can be derived from non-standard Lagrangians. The obtained results are used to obtain non-standard Lagrangians for several ODE's of special interest in applied mathematics.
The hyperbolic plane is a plane where every point is a saddle point. Because of Hilbert's theorem, we have believed it impossible to isometrically immerse a complete hyperbolic plane in three-dimensional Euclidean space. There are, however, many useful models of hyperbolic geometry in Euclidean space where the metric is not preserved. Crocheting is a method of creating fabric by interlocking loops of yarn, thread, or strands of other materials through use of a crochet hook. Because this method requires loops to be done one at a time from a single point, crocheting is a great means to represent the hyperbolic plane.
The project includes the formulation of a paper-folding scheme to cut out any triangle drawn on a piece of paper with one slice of the scissors. The development of the method, demonstrations of the method, a mathematical proof of why the method works, the geometrical properties and patterns observed, an extension of the method to other polygons, and a trick to rig the polygon into breaking the method will be presented.
Inverse semigroups are algebraic objects that generalize groups. We will study properties of the inverse semigroup through the centralizer of the idempotents and its Munn quotient. In particular, we characterize exactly when the Munn quotient is E-unitary. This research was conducted at the 2016 REU at University of Texas at Tyler.
Principal Component Analysis (PCA) is a statistical procedure that uses an orthogonal transformation to convert a set of observations of possibly correlated variables into a set of values of linearly uncorrelated variables called principal components, which are vectors in the data that signify the most variance. PCA has numerous applications, one of which is facial recognition. We will discuss the process involved in achieving facial recognition via PCA as well as demonstrate its results.
The introduction of this paper is to introduce the basic components of the knot Theory. After understanding the concept of mathematical knots, we will project mathematical knots in order to determine the factors in the knots neurons create while the brain acts a certain way based on the action demonstrated by an individual. We will calculate a different tangle, knot crossings created inside a human brain showing why everyone's brain is shaped with so many wrinkles. This will eventually help you understand how you can use this method on determining whether the shape of several neuron patterns can distinguish the perfect activity outcome of an individual. This research will also introduce several new techniques on observing the wrinkles in a human brain also known as the sulci and gyri. Instead of calling the sulci and gyri by its physical property name we will call them mathematical strands to project the crossings between several brains and how the gure created based on the neuron movement can conclude whether the activity initiated will be a successful one or not. We will begin by using the temporal lobe and the occipital lobe and virtual cross the two to the parietal lobe in order to perform a form of knot.
There is an understanding that someone can create a formula from a team's' statistical data to generate a perfect bracket. This is done for many sports such as baseball, football, soccer, and basketball. The method of using a win-to-loss ratio can be unreliable because of many unknown variables. In this research we will reproduce what sports analysts have done and introduce it into the National Hockey League (NHL). By gathering data and entering it into a matrix to generate a ranking system, we will theoretically be able to produce the perfect bracket of the Stanley Cup winners for 2016. We will utilize the Colley method to manipulate matrices to rank teams by reducing a matrix into reduced echelon form thus producing the ranks of each team. In this method we will created a point system which the win-to-lose ratio and the number of times each team played each other coincides to each other. To add different varying results, in attempt to improve on the bracket, we will introduce point differentials by multiplying by or adding to the point system in the Colley method. From the data collection we will deduce who is the future Stanley Cup Champion.
American Roulette is a casino game. A player places a bet on a set of numbers according to specific types of bets for the game. The croupier then spins a wheel with 38 numbers on it and drops a small ball into the wheel, which slows with the ball stopping on a single number. Whoever placed a bet on the number or color wins, with a payout multiplier that differs for each type of bet. As a result it is difficult to gauge which bet to place in order to reach whatever goal has been set by the player. Using Markov chains, however, we compute a gambler's probability of success and length of the game.
Suppose a mathematician was playing darts using Pascal's triangle with infinitely many rows as a dart board. What is the probability that the mathematician's dart will land on an even number? To find the probability of hitting an even number simply divide the number of even numbers by the number of numbers. Since the board has an infinite number of rows, numbers will be modeled by equations and a limit will be used to calculate the probability. As the number of rows gets arbitrary large, the probability of hitting an even number gets arbitrarily close to one. If the mathematician were trying to hit a multiple of a different number, new probabilities must be calculated.
In elections with two candidates it is common to use majority rule, a voting method in which the candidate who receives the most votes wins. The intuitive fairness of majority rule is confirmed by a result known as May's theorem, which proves that in elections with two candidates, majority rule is the unique voting method satisfying certain "fairness conditions". Elections with three or more candidates are substantially more complicated, and it has been proven that there are no voting methods satisfying all the fairness conditions that one would like to impose. Consequently, in elections with multiple candidates, different voting methods are used depending on which fairness criteria are most relevant in a given situation. In this talk we introduce a new voting method for elections with multiple candidates in which the winner is determined by minimizing collected voter unhappiness. We consider several properties of this new voting method and examine situations for which this method is appropriate.
Type 2 diabetes is one of the leading causes of death in America. This type of diabetes is caused by insulin resistance which disables your body's ability to properly regulate your blood sugar levels. Having high blood sugar levels causes inflammation within the body, which eventually leads to organ failure. TNF-alpha, also known as tumor necrosis factor alpha, is a specific cell signaling protein involved in inflammation and insulin resistance inside the body. In this project, we analyze the protein-protein interaction (PPI) network of TNF-alpha by using graph theory in order to understand more about inflammatory pathways found in the development of type 2 diabetes.
The symmetric inverse monoid, SIM(n), is the set of all partial one-to-one mappings from the set {1,2,…,n} onto itself under the operation of composition. Earlier research on the symmetric inverse monoid delineated the process for determining whether an element of SIM(n) has a k-th root. The problem of enumerating k-th roots of a given element of SIM(n) has since been posed, which we aim to solve. Previously, I enumerated k-th roots of the Symmetric Group, an important submonoid of SIM(n), and will enumerate the k-th roots of any element of SIM(n) in this presentation.
As higher education costs continue to rise, many students, faculty, and institutions are looking for ways to bend the cost curve downward. In this talk, we will explore several easy-to-use and powerful, yet free, resources for faculty and students to use in classes of various levels and styles.
Some real-life applications of linear algebra can be found in most digital image editing software. In this research project, my teammate and I have completed a few tutorials in which we defined a matrix and used the singular value decomposition (SVD) to compress and image matrix by reducing the amount of eigenvalues. In order to complete this process, we used the mathematics engine MATLAB to compile the code necessary to compress an image to our specifications allowing us to control the number of eigenvalues. After writing the code, we used LaTeX to create a tutorial for classroom instruction or for use of use of reference for those seeking further insight or instruction on this topic. Once completed, we presented our tutorial in a classroom setting and gathered feedback from the students that could be used to improve future tutorials by using Google Forms. We plan on creating more tutorials in the future using the feedback that we receive from current students.
Many students struggle to visualize the geometric properties of 3D vectors. To this point, these concepts have been taught by drawing a 2D representation on a whiteboard or paper to represent this 3D concept. Sometimes professors will use online 3D modeling software. This does give a better picture, but is still a 2D representation of a 3D concept. For many students, this representation is confusing and does not help them visualize these concepts. For this project, I have created a prototype of a physical model of the three dimensional vector space using 3D printing that can be used to teach the geometric properties of 3D vectors and vector operations. I administered a pre-assessment to students in a Calculus 2 class that was taught using traditional methods in Fall 2015. I then used this model in a Linear Algebra class and a Calculus 2 class in Spring 2016. I gave the same assessment to the Calculus 2 class that was taught using the model in the Spring. In this talk, I will discuss my process of creating the model and present my preliminary findings from the assessments.
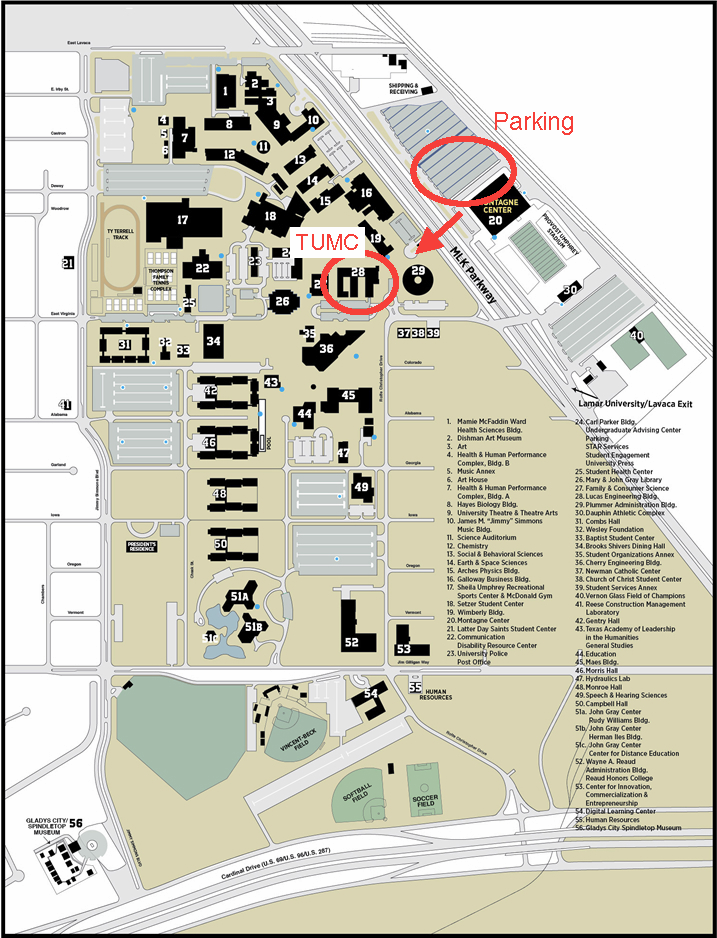
Click the map for a printable PDF version.
Registration and Abstract Sumbmission
Registration is now closed. The deadline for registration and abstract submission was September 26, 2016.
Registration fees are $15 for students and $35 for faculty. Checks for registration fees should be made out to Lamar University and mailed to Dr. Jacqueline Jensen-Vallin at the address below. Please contact Dr. Jensen-Vallin at jacqueline.jensen@lamar.edu with any questions or concerns.
Dr. Jacqueline Jensen-Vallin
Editor, MAA FOCUS
Associate Professor
Mathematics Department
200F Lucas Building
PO Box 10047
Lamar University
Beaumont, TX 77710
Hotel Information & Room List
Students who registered before September 26th are being provided housing at the conference hotel, the Holiday Inn at I-10 and Walden. The room list can be found here. Please let us know if your name does not appear. Faculty are expected to make their own housing arrangements.
The hotel offers breakfast with the rooms. Some morning snacks will be provided at the conference, but it will not be a full breakfast.
Holiday Inn Hotel & Suites Beaumont-Plaza
3950 I-10 South & Walden Rd.
Beaumont, Texas 77705
409.842.5995


