A total of 103 Michigan high school students, from 53 different schools, were honored for their achievements on the 41st Annual Michigan Mathematics Prize Competition at the Awards Day program held on February 28 at Michigan State University. Jerry Ludden (MSU) is this year's director of the MMPC.
Professors Mary Winter and Sheldon Newhouse (MSU) presented stimulating talks in the afternoon to the award winners and their families and high school mathematics teachers. Both presentations dealt with geometry, fractals, and chaos, and the students also had an opportunity for some hands-on work with relevant software. Vijay Divi (a student from Troy High School) spoke at the awards banquet about his experiences last year in the ARML competition, in which teams drawn from the Top 100 compete in mathematics problem solving against other top teams from around the country. The 1998 contest will take place on May 30 at the University of Iowa, and three spring practice sessions around the state will prepare team members. Michigan teams have consistently done well in this event (see report in the Fall Newsletter).
This year's first, second, and third place Gold award recipients were Michael Khoury, Jr. (Brother Rice), Robert Easton (Lapeer West), and Vijay Divi (Troy), respectively. First Level Silver winners were Robert Lillibridge (Livonia MSC) and Qian Zhang (Livonia MSC); the Second Level Silver award went to Goutam Reddy (Detroit County Day); and Third Level Silver awards were captured by Haiwen Chu (Andover), Betsy Huebner (Grosse Pointe North), Ryan Lang (L'Anse Creuse), and Thomas Chambers, III (Royal Oak Kimball). An additional 46 students received Bronze awards, and 47 received Honorable Mentions.
The top 56 students received over $30,000 in scholarships, in amounts ranging from $450 to $2500, thanks to generous funding of the MMPC by corporate and other donors. The Honorable Mention winners received a copy of the book Mathematical Gems, III.
Part I of this year's MMPC (a 40-question multiple choice test) was administered to about 15,000 students in October. The top 1000 students took Part II in December.
Next year the MMPC will stay at MSU. Make sure to plan on helping with the grading next January 9 in East Lansing!
MMPC Top 103 Statistics
- Top Gold winner Michael Khoury, Jr., is a junior. Second place winner Robert Easton and third place winner Vijay Divi are seniors.
- Among the seven Silver winners are four seniors, two juniors, and one sophomore.
- Among the 46 Bronze winners are 22 seniors, 15 juniors, five sophomores, two freshmen, and two eighth-graders.
- Twenty-five seniors, 14 juniors and eight sophomores took Honorable Mentions.
- There were 12 females among the Top 103 (one Silver, seven Bronze, and four Honorable Mentions).
- The highest score was 92 out of 100. The cutoff score for scholarships was 65. It took a 60 to make it into the Top 103.
- Of the roughly 15,000 students from about 500 schools who took Part I, 1050 students from 157 schools qualified for Part II by scoring 21 or higher (out of 40).
41st MMPC Part II Problems
The top 1000 students had 100 minutes to solve these five problems and compete for scholarships and recognition.
- It can be shown in Calculus that the area between the
x-axis and the parabola y = k x2
(k a positive constant) on the interval 0<=x<=a
is k a3 / 3.
- Find the area between parabola y = 4x2 and the x-axis for 0 <= x <= 3.
- Find the area between parabola y = 5x2 and the x-axis for -2 <=x<= 4.
- A square 2 by 2 dartboard is situated in the xy-plane with its center at the origin and its sides parallel to the coordinate axes. Darts that are thrown land randomly on the dartboard. Find the probability that a dart will land at a point of the dartboard that is nearer to the point (0,1) than to the bottom edge of the board.
- When two rows of a determinant are interchanged, the value of
the determinant changes sign. There are also certain operations which can
be performed on a determinant which leave its value unchanged.
Two such operations are changing any row by adding a constant multiple of
another row to it, and changing any column by adding a constant multiple of another
column to it. Often these operations are used to generate lots of zeroes
in a determinant in order to simplify computations. In fact, if we can
generate zeroes everywhere below the main diagonal in a determinant, the value
of the determinant is just the product of all the entries on that main diagonal.
[An example was given.] Transform these determinants into
determinants with zeroes everywhere below the main diagonal, and find their values:
(a) 1 3 -1 (b) 0 1 2 3 4 7 2 1 0 1 2 3 -6 5 2 1 0 1 3 2 1 0 - In Pascal's triangle, the entries at the ends of each row are both 1,
and otherwise, each entry is the sum of the two entries diagonally above it:
Row number 0 1 1 1 1 2 1 2 1 3 1 3 3 1 4 1 4 6 4 1The triangle gives the binomial coefficients in expansions like (a + b)3 = 1a3 + 3a2b + 3ab2 + 1b3.- What is the sum of the numbers in row #5 of Pascal's triangle?
- What is the sum of the numbers in row #n of Pascal's triangle?
- Show that in row #6 of Pascal's triangle, the sum of all the numbers is exactly twice the sum of the first, third, fifth, and seventh numbers in the row.
- Prove that in row #n of Pascal's triangle, the sum of all the numbers is exactly twice the sum of the numbers in the odd positions of that row.
- The product of several terms is sometimes described using the
symbol , which is capital pi, the Greek equivalent of p, for the word "product".
For example, the symbol Pk=1..4
(2k+1) means the product of numbers of the form
(2k+1), for k = 1,2,3,4. Thus it equals 945.
- Evaluate as a reduced fraction Pk=1..10 k /(k+2).
- Evaluate as a reduced fraction Pk=1..10 (k2 + 10k + 17) /(k2 + 14k + 41).
- Evaluate as a reduced fraction
Pk=1..
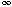 (k3
1)/(k3 + 1).
(k3
1)/(k3 + 1).
- In right triangle CAB (right angle at A), the median AF, the angle bisector AE, and the altitude AD divide the right angle A into four equal angles, where F, E, and D occur in that order on the line segment from C to B. If AB = 1, find the area of triangle AFE.
- If in any triangle, an angle is divided into four equal angles by the median, angle bisector, and altitude drawn from that angle, prove that the angle must be a right angle.
Out of the Mouths of Budding Mathematicians
This year's MMPC Part II produced the usual collection of humorous remarks which the graders dutifully recorded. Here is a selection from among them, culled by Exam Committee Chair Mike Merscher (LTU).
"The area of the triangle is 148 pounds."
"The answer is between 0 and 7/9. That should be worth 4 points credit."
"I should know this, but we skipped that chapter."
"You obviously believe this is true, and that's okay. I just don't understand why you need my support."
"This seems hard, but it is actually very easy, because the product of an infinite amount of numbers is zero."
"This is a big math test. A big math test would not ask us to prove that a false statement is true. Therefore the statement is true."
"The angle bisector divides the angle into two equal but quite different angles."
"I have a wonderful proof, and I'd like to show it to you, but I have to go to Lit class."
"The dart will probably have a low probability of landing nearer the point than the bottom edge of the dartboard, because most people tend to shoot right at where they want the dart to land and neglect to consider that gravity pulls down on the dart at 9.8 meters per second per second."