47th MMPC Part II Problems

The top 1,013 students had 100 minutes to solve these five problems.

1. Consider the equation x₁x₂ + x₂x₃ + ... + x_n–1x_n + x_nx₁ = 0 where x_i = 1 or –1, for i = 1,2, ..., n.
   1. Show that if the equation has a solution, then n is even.
   2. Suppose that n is divisible by 4. Show that the equation has a solution.
   3. Show that if the equation has a solution, then n is divisible by 4.
2. 1. Find a polynomial f(x) with integer coefficients and two distinct integers a and b such that f(a) = b and f(b) = a.
   2. Let f(x) be a polynomial with integer coefficients and a, b, and c be three integers. Suppose that f(a) = b, f(b) = c, and f(c) = a. Show that a = b = c.
3. 1. Consider the triangle with vertices M(0,2n+1), S(1,0), and U(0,1/(2n²)), where n is a positive integer. If θ is the angle MSU, prove that tan θ = 2n–1.
   2. Find positive integers a and b that satisfy the following equation. arctan(1/8) = arctan a – arctan b
   3. Determine the exact value of the following infinite sum. arctan(1/2) + arctan(1/8) + arctan(1/18) + arctan(1/32) + … + arctan(1/(2n²)) + …
4. 1. Prove: (55 +12(21)^1/2)^1/3 + (55 – 12(21)^1/2)^1/3 = 5.
   2. Completely factor x⁸ + x⁶ + x⁴ + x² + 1 into polynomials with integer coefficients, and explain why your factorization is complete.
5. 
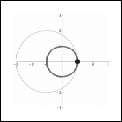
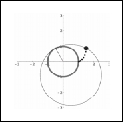
   In this problem, we simulate a hula hoop as it gyrates about your waist. We model this situation by representing the hoop with a rotating circle of radius 2 initially centered at (–1,0), and representing your waist with a fixed circle of radius 1 centered at the origin. Suppose we mark the point on the hoop that initially touches the fixed circle with a black dot (see the left figure). As the circle of radius 2 rotates, this dot will trace out a curve in the plane (see the right figure). Let θ be the angle between the positive x-axis and the ray that starts at the origin and goes through the point where the fixed circle and the circle of radius 2 touch. Determine formulas for the coordinates of the position of the dot, as functions x(θ) and y(θ). The left figure shows the situation when q = 0 and the right figure shows the situation when θ = 2π/3.

Back to the Spring Newsletter

This page is maintained by Earl D. Fife