Grinnell College
March 13, 1999
Problems by A. M. Fink, Iowa State University

Problerns 1-8 are worth 10 points. Problem 9 is worth 20 points.

1.   Let  f (x) have two continuous derivatives on R.
      Show that either there is a point x such that  f (x) f '(x) f "(x) = 0 or that f (x) f "(x) > 0 for all x in R.

2.   If two people shake hands, then each of them has shaken one hand. If at some succeeding time they again shake hands, then each has shaken hands twice, etc. For each person who is alive or has ever lived, consider the total number of times he/she has shaken hands. Show that at any time, the number of people (living or dead) who have shaken hands an odd number of times is even.

3.   Find the smallest period of  f  where f (x) = 4 cos ³ x - 3 cos x.

4.   Graph, without use of a calculator,  y = f (x) where
                                        

5.   Without using L'Hopital's, show that for any real n,

                                     

6.   Let the IQ of a triangle be the ratio

                                          area of the triangle
                                    (perimeter of the triangle)²

This is a dimensionless number. Show that the smartest triangles are equilateral triangles.

7.   A Morse code message is a string of dots and dashes. The length of such a message is defined to be:
                                                 the # of dots + 2(the # of dashes)

Messages are determined uniquely by the number of dots and dashes and by the order of the dots and dashes. How many distinct messages are there of length 20? Your answer should be given as an explicit integer in decimal form.

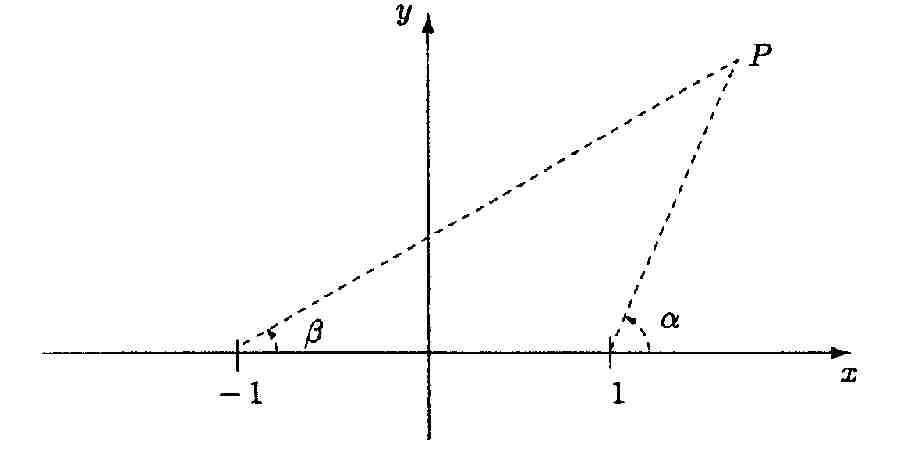
8.   Let P be a point in the plane that is neither (1, 0) nor (-1, 0). Let  be the smallest non-negative angle (i.e., measured in the counter-clockwise direction) between the positive x-axis and the line segment from (1, 0) to P, and  the smallest non-negative angle between the positive x-direction and the line segment from (-1, 0) to P. Thus,  and  are both in
[0, 2). See the figure below.

a. Find all points in the plane such that  +  = / 2.

b. Find all points in the plane such that  +  = .

9.   Let N be the set of positive integers. Define a function  f  : N   N as follows:
            if n = d_kd_k-1. . .d₂d₁d₀ is the decimal expansion for n, (with each d_i a digit between 0 and 9), then

                                                    f (n) = d₀²  + d₁² + . . . + d_k² .

    Thus, f (n) is the sum of the squares of the digits of  n, e.g.,  f (345) = 3² + 4² + 5² = 50.

Define a dynarnical system on N by iterating the function f , i.e., start with an n and compute in turn, f (n),  f (f(n)),
f (f (f (n))), etc. This sequence is call the orbit of the number n.  For example

                345   f (345) = 50   f (50) = 25   f (25) = 29   f (29) = 85    . . .

a. Show that all orbits eventually enter the interval [1, 162].
b. Show that all orbits which start in [1,162] stay there.
c. The trivial interval [1,1] satisfies f ([1, 1]) = [1,1], and part b. above shows that f([1, 162]) = [1,162]. These intervals are called invariant intervals. Show that there is no n, 2  n  161, such that [1, n] is an invariant interval.
d. Find an orbit that is periodic with period greater than 1. (An orbit is periodic if the elements of the orbit repeat. The period of an orbit is the length of the shortest repeating block in the orbit.)
e. Find nine numbers n < 162 for which the orbit of n converges to 1.