Fourth Annual Iowa Collegiate Mathematics Competition

Iowa State University
April 4, 1998
Problems by Paul Zeitz, University of San Francisco (zeitz@usfca.edu)

The problems below are listed in roughly increasing order of difficulty. Each problem requires proof or justification. An answer alone is not sufficient. Calculators are permitted, but not particularly useful.

1.  How Unlucky Can You Get?

What are the maximum number of "Friday the l3ths" that can occur in a normal 365-day year? What are the minimum number that must occur? (Recall that April, June, September and November each have 30 days, February has 28 days, and all the other months have 31 days.)

2.  Break it Up!

Two people take turns breaking up a rectangular chocolate bar which starts as 6 x 8 squares in size. Players alternate turns. For a turn, a player takes one of the pieces of chocolate consisting of two or more squares and breakes it into two pieces. Breaks can only made along a division between the squares and each break must be a straight line. For example, you can turn the original bar into a
6 x 2 piece and a 6 x 6 piece, and this latter piece can be turned into a 2 x 6 piece and a 4 x 6 piece. The last player who can (legally) break the chocolate wins (and gets to eat the chocolate bar). Is there a winning strategy for the first or second player? What about the general case (the starting bar is m x n)?

3.  Worlds in Collision

A bubble-chamber contains three types of sub-atomic particles: 1998 particles of type X, 2002 of type Y, 2003 of type Z. Whenever an X- and Y- particle collide, they both become Z-particles. Likewise, Y- and Z- particles collide and become X-particles and X- and Z- particles become Y-particles upon collision. Can the particles in the bubble chamber evolve so that only one type is present?

4.  Rendezvous at Noon

Two towns, A and B, are connected by a road. At sunrise, Pat begins biking from A to B along this road, while simultaneously Dana begins biking from B to A. Each person bikes at a constant speed, and they cross paths at noon. Pat reaches B at 5 pm while Dana reaches A at 11:15 pm. When was sunrise?

5.  Ten Random Numbers

A random number generator outputs integers from the set {1,2,3,4,5,6,7,8}, with each of the eight choices equally likely. If ten such random integers are created, what is the probability that their product is one more than a multiple of 8?

6.  A Bug's Journey

A bug is crawling on the coordinate plane from (7,11) to (-17, -3). The bug travels at constant speed one unit per second everywhere but quadrant II (negative x- and positive y- coordinates), where it travels at 1/2 units per second.  What path should the bug take to complete its journey in minimal time?

7.  Invariance under Iteration

Let f: [0,1] ® [0,1] be defined by

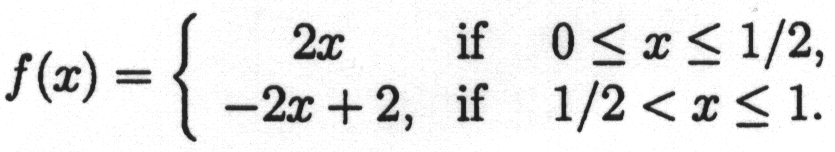
Next, create a sequence of functions from [0,1] to [0,1] as follows:   Let f₁(x) = f (x) and
let f_n(x) = f ( f_n-1 (x) ) for n > 1.   Prove that

8.  Independent Vectors

Let A be an n x n matrix with real entries, and let v Rⁿ be a vector which satisfies A^mv = 0 and A^m-1v0 for some positive integer m.  Show that the m vectors   v,  Av,  A²v, . . . ,  A^m-1v  are linearly independent.

9.  A Positive Polynomial

Let p(x) be a polynomial with real coefficients of even degree whose coefficient of highest degree is positive. Suppose also that p(x) p"(x) for all real x.   Show that p is non-negative, that is,
p(x) 0 for all real x.

10.  An Irrational Conclusion

Prove that the sum  is irrational.