Third Annual Iowa Collegiate Mathematics Competition

Grinnell College
April 5, 1997
Problems by Stan Wagon, Macalester College (wagon@macalester.edu)

Proof or justification is required. When a problem asks you to find something, you should find it and prove that it does the job: it is not sufficient to simply state an answer. Calculators (vanilla, graphing, or programmable) are allowed and might be useful.

1. You Deserve a Break Today

What is the largest number such that no combination of Chicken McNugget buckets will yield exactly that number of McNuggets?

2. Black and White and Black and . . .

Draw some (doubly infinite) lines in the plane and color the regions alternately black and white (i.e., regions that share a boundary line get different colors). Often the number of black regions equals the number of white regions. Sometimes the black number can exceed the white number by one (or vice versa). Is it possible for this discrepancy to be two?

3. The Big Wheel

Imagine a gigantic solid wheel 100 miles in radius rolling along a flat surface at 60 miles per hour. You are behind a square window 6 feet on a side that lies on the surface (see diagram, which is not drawn to scale). When the wheel rolls by, your win dow is darkened for a while. How much time (to the nearest second) elapses while the wheel is darkening all or part of your window? NOTE. There are 5280 feet in one mile.

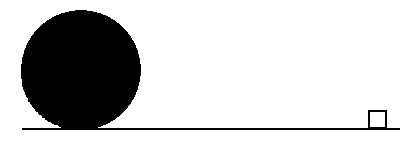
4. A Fibonacci Puzzle

It is easy to find three Fibonacci numbers that form an arithmetic progression. Prove that there are no four Fibonacci numbers that form an arithmetic progression.

5. Alice's Mysterious Linear Equations

ALICE: "I'm thinking of some numbers. Can you tell what they are?"
BOB: "Give me a break! I need more information than that."
ALICE: "Okay. They form a solution to a system of n linear equations in n unknowns."
BOB: "That's not much help."
ALICE: "The system has only one solution."
BOB: "Lots of systems have only one solution."
ALICE: "All right, the system's coefficients and constant terms form an arithmetic progression." BOB: "You mean like 2x + 5y + 8z = 11, 14x + 17y + 20z = 23, and 26x + 29y + 32z = 35?" ALICE: "That's right."
BOB (after a pause): "Well, then your numbers must be _______________
ALICE: "Right!"

6. The Electrician's Dilemma

A tunnel underneath a large mountain range serves as a conduit for 100 identical wires; thus, at each end of the conduit, one sees 100 wire-ends. Your job is to label all the ends with labels #1, #2,. .. ,#l00, so that each wire has the same label at its two ends.

You may join together arbitrary groups of wires at either end; they will then conduct electricity through the join. Then you cross the mountains by a very expensive and dangerous helicopter ride to the other end, where you can feed electricity through any wire and check which of the other ends are live, attach notes to the wires, and make (or unmake) connections as desired. Then you fly back to the near end, perform the same sort of operations, fly back, and so on as often as required.

How can you accomplish your task with the smallest number of helicopter flights?

7. Decomposing a Googol

Can a googol (10¹⁰⁰) be written as n² - m², where n and m are positive integers?

8. A Special Quadratic

There is a quadratic polynomial with a, b, c integers and such that if n consists only of is when written in base 10, then the same is true of P(n). Find such a quadratic.

9. Martian Artifacts

You have just landed on Mars where you find 7 identical-looking spheres. But, from prior missions, you know the following:

Each sphere is colored on the inside. One of the colors occurs for a strict majority of the spheres (4 or more). When two spheres of the same color touch each other, they both glow.

Your job is to carry out as few comparisons as possible, with the goal of holding in your hand a sphere that you are certain has the majority color. What is the smallest number of comparisons that is guaranteed to work?

10. An Exponential Integral

The value of can be expressed as a.bc...× 10^m, where m is a positive integer and a is
one of 1, 2, 3,..., 9.

(7 points) (a). What is m?
(3 points) (b). What is a?