Second Annual Iowa Collegiate Mathematics Competition

Iowa State University
March 30,1996
Problems by Leo Schneider

1. Leo Bikes

Leo can drive, bicycle, or walk from home to school in the morning.

• The drive takes 20 minutes.
• If he uses his bicycle, the trip takes 45 minutes.
• Once upon a time he walked, and it took him 2.5 hours.

The evening before Leo has an important class at 8AM the next morning, the TV weather person makes it sound as though the next morning will be an ideal one for biking to school. Although Leo's bicycle is currently working perfectly, it has recently had frequent repair problems at random times.

Leo plans to bicycle to school the next morning. If the bicycle breaks down enroute, from the point of the breakdown he will either

• walk the rest of the distance to school, or
• walk back home and drive to school,

whichever will get him to school most quickly.

(a) What is the latest minute (integer) when must Leo leave home the next morning to insure he will be at school at or before 8AM. even if his bike stops working someplace enroute?

(b) Suppose that he leaves at the time you specify in (a).  He needs a plan of action in case his bicycle breaks down on the way to school at v:wx:yzAM. Give a time a:bc:deAM, to the nearest second, such that if the breakdown occurs at or before a:bc:deAM his fastest way to school is to return home and get the car, and if the breakdown occurs after a:bc:deAM his fastest way to school is to continue on to school by foot.

Be sure to show your mathematical work justifying your answers to (a) and (b).

2. Dodecagon Diagonals

Let ABCDEFGHIJKL be a regular 12-sided polygon.

Prove or disprove: The diagonals , , and  intersect in a point.

3. Fractions from Sequences

Suppose a₁, a₂, a₃, …, is a non-constant arithmetic sequence* of real numbers, and define the sequence b₁, b₂, b₃, … by the rule

Assume that the a_i are such that the denominator of b_n is never 0.

(a) Describe, with proof, the set of all possible real numbers L for which

(b) Describe, with proof, those non-constant arithmetic sequences,

for which the sequence

is a constant sequence.

*REMINDER: An arithmetic sequence (or arithmetic progression) is a sequence for which there is a constant such that each term after the first can be obtained by adding that constant to the preceding term.

4. Determinants of Functions

When this sum of determinants

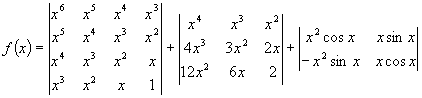
is expanded and simplified, it is a polynomial in terms of x.

What is the degree of this polynomial? Justify your answer!

5. Intersecting Segments

Find, with proof, a polynomial in 8 variables,

and a permutation (k₁, k₂, k₃, k₄, k₅, k₆, k₇, k₈) of (a, b, c, d, e, f, g, h) so that:

the line segment in the xy-plane from (a, b) to (c, d)
has at least one point in common
with the line segment from (e, f) to (g, h).

6. Prime Divisors of a Binomial Coefficient

Find the largest prime whose square divides the binomial coefficient

Justify your answer.

7. Walking the Streets

Consider the grid on the plane consisting of all vertical lines with equations x = i for i an integer and all horizontal lines with equations y = j for j an integer as a pattern of streets in a town. There are many paths along these streets that are 20 units long and connect (0,0) to (10,10).

(a) How many of these paths avoid the intersection (3,5), which is said to be a very
dangerous intersection? Justify your answer.

(b) There is a railroad track that approximately follows the line y = x. The area of town where y > x is said to be "the other side of the tracks". There is a great ice cream store at (7,1). If you decide to walk from (0,0) to (10, 10), avoiding the tracks and the other side of the tracks and stopping for an ice cream cone on the way, how many paths can you choose from? That is, how many paths of length 20 from (0,0) to (10,10) pass through (7,1) and go through only intersections (i,j) with j < i between the two endpoints? Justify your answer.

8. Hexadecimal 17 Casting

Hexadecimal (base sixteen) numerals are written using the digits 0 through 9 and A = ten,
B = eleven, C = twelve, D = thirteen, E = fourteen, and F = fifteen. Design a simple algorithm to determine whether or not a positive integer N is evenly divisible by 17, where the algorithm is based on the hexadecimal digits and their positions in the hexadecimal numeral for N.
Explain why the algorithm works!

Hint: You know the rule for summing the digits of a base 10 number to see whether or not it is divisible by 9. This is a similar, though not identical, algorithm based on digits.

9. Bug on a Tetrahedron

A bug takes a random walk on the edges of a regular tetrahedron ABCD. Whenever the bug arrives at a vertex, it makes a random choice of one of the three edges emanating from that vertex and walks to the vertex at the other end of that edge. The bug starts at vertex A. Write a formula f(n), in terms of n, which gives the probability that the bug is back at vertex A after traversing n edges. Justify your answer.

10. How Small?

Find a twice continuously differentiable function y = f(x) which is not identically zero on the interval [0,1] but for which f(0) = 0 = f(1) and which makes

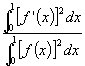
as small as you can make it.

This problem will be "graded on a curve": the smaller your value for that quotient of integrals, the better the grade. Of course, if you find what you feel must be the smallest possible value and prove it, that could be worth one extra credit point.